How Do You Know if a Bond Has a Dipole Moment
Dipole Moments
- Page ID
- 1323
Dipole moments occur when there is a separation of charge. They tin can occur between two ions in an ionic bond or between atoms in a covalent bond; dipole moments arise from differences in electronegativity. The larger the difference in electronegativity, the larger the dipole moment. The distance between the charge separation is also a deciding factor into the size of the dipole moment. The dipole moment is a measure of the polarity of the molecule.
Introduction
When atoms in a molecule share electrons unequally, they create what is called a dipole moment. This occurs when one atom is more electronegative than another, resulting in that atom pulling more than tightly on the shared pair of electrons, or when ane cantlet has a lone pair of electrons and the difference of electronegativity vector points in the same way. One of the about common examples is the water molecule, made up of one oxygen cantlet and ii hydrogen atoms. The differences in electronegativity and alone electrons give oxygen a partial negative charge and each hydrogen a partial positive charge.
Dipole Moment
When two electrical charges, of opposite sign and equal magnitude, are separated by a distance, an electric dipole is established. The size of a dipole is measured by its dipole moment (\(\mu\)). Dipole moment is measured in Debye units, which is equal to the altitude between the charges multiplied past the charge ( one Debye equals \(3.34 \times 10^{-30}\; C\, m\)). The dipole moment of a molecule can be calculated past Equation \(\ref{1}\):
\[ \vec{\mu} = \sum_i q_i \, \vec{r}_i \label{1}\]
where
- \(\vec{\mu}\) is the dipole moment vector
- \(q_i\) is the magnitude of the \(i^{th}\) charge, and
- \(\vec{r}_i\) is the vector representing the position of \(i^{th}\) charge.
The dipole moment acts in the direction of the vector quantity. An example of a polar molecule is \(\ce{H_2O}\). Because of the lone pair on oxygen, the structure of \(\ce{H_2O}\) is bent (via VEPSR theory), which that the vectors representing the dipole moment of each bond practise not abolish each other out. Hence, water is polar.

The vector points from positive to negative, on both the molecular (net) dipole moment and the private bond dipoles. Table A2 shows the electronegativity of some of the mutual elements. The larger the difference in electronegativity between the two atoms, the more electronegative that bond is. To be considered a polar bond, the divergence in electronegativity must be big. The dipole moment points in the management of the vector quantity of each of the bond electronegativities added together.
It is relatively piece of cake to measure dipole moments; but place a substance between charged plates (Figure \(\PageIndex{two}\)) and polar molecules increment the charge stored on plates and the dipole moment can exist obtained (i.e., via the capacitance of the arrangement). Nonpolar \(\ce{CCl_4}\) is non deflected; moderately polar acetone deflects slightly; highly polar water deflects strongly. In general, polar molecules volition align themselves: (one) in an electric field, (2) with respect to one another, or (3) with respect to ions (Figure \(\PageIndex{2}\)).
Equation \(\ref{1}\) can be simplified for a simple separated two-accuse system like diatomic molecules or when because a bail dipole inside a molecule
\[ \mu_{diatomic} = Q \times r \characterization{1a}\]
This bond dipole is interpreted as the dipole from a charge separation over a distance \(r\) between the partial charges \(Q^+\) and \(Q^-\) (or the more unremarkably used terms \(δ^+\) - \(δ^-\)); the orientation of the dipole is forth the centrality of the bond. Consider a unproblematic organisation of a single electron and proton separated by a fix distance. When proton and electron shut together, the dipole moment (degree of polarity) decreases. However, every bit proton and electron get farther autonomously, the dipole moment increases. In this case, the dipole moment calculated as (via Equation \(\ref{1a}\)):
\[\begin{align} \mu &= Qr \nonumber \\[4pt] &= (one.lx \times 10^{-xix}\, C)(1.00 \times ten^{-10} \,grand) \nonumber \\[4pt] &= i.60 \times ten^{-29} \,C \cdot m \characterization{2} \end{align}\]
The Debye characterizes size of dipole moment. When a proton & electron 100 pm apart, the dipole moment is \(iv.80\; D\):
\[\begin{align} \mu &= (1.sixty \times 10^{-29}\, C \cdot k) \left(\dfrac{1 \;D}{iii.336 \times 10^{-30} \, C \cdot m} \correct) \nonumber \\[4pt] &= iv.eighty\; D \characterization{3} \end{align}\]
\(4.80\; D\) is a key reference value and represents a pure charge of +1 and -i separated past 100 pm. If the charge separation were increased then the dipole moment increases (linearly):
- If the proton and electron were separated past 120 pm:
\[\mu = \dfrac{120}{100}(4.80\;D) = 5.76\, D \characterization{4a}\]
- If the proton and electron were separated by 150 pm:
\[\mu = \dfrac{150}{100}(4.eighty \; D) = 7.20\, D \characterization{4b}\]
- If the proton and electron were separated by 200 pm:
\[\mu = \dfrac{200}{100}(4.80 \; D) = nine.threescore \,D \label{4c}\]
Instance \(\PageIndex{ane}\): H2o
The h2o molecule in Figure \(\PageIndex{1}\) tin be used to make up one's mind the management and magnitude of the dipole moment. From the electronegativities of oxygen and hydrogen, the difference is 1.2e for each of the hydrogen-oxygen bonds. Next, because the oxygen is the more electronegative atom, it exerts a greater pull on the shared electrons; it too has two alone pairs of electrons. From this, it can be concluded that the dipole moment points from between the two hydrogen atoms toward the oxygen atom. Using the equation in a higher place, the dipole moment is calculated to be one.85 D by multiplying the altitude between the oxygen and hydrogen atoms by the charge difference between them and then finding the components of each that bespeak in the direction of the net dipole moment (the angle of the molecule is 104.five˚).
The bond moment of O-H bond =one.five D, so the net dipole moment is
\[\mu=two(ane.5) \cos \left(\dfrac{104.5˚}{2}\correct)=1.84\; D \nonumber\]
Polarity and Structure of Molecules
The shape of a molecule and the polarity of its bonds decide the OVERALL POLARITY of that molecule. A molecule that contains polar bonds, might non have whatever overall polarity, depending upon its shape. The simple definition of whether a complex molecule is polar or not depends upon whether its overall centers of positive and negative charges overlap. If these centers lie at the same point in space, then the molecule has no overall polarity (and is non polar). If a molecule is completely symmetric, then the dipole moment vectors on each molecule will abolish each other out, making the molecule nonpolar. A molecule can just be polar if the structure of that molecule is not symmetric.
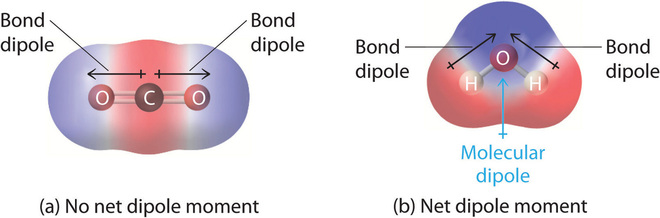
A proficient instance of a nonpolar molecule that contains polar bonds is carbon dioxide (Effigy \(\PageIndex{3a}\)). This is a linear molecule and each C=O bail is, in fact, polar. The central carbon will accept a net positive accuse, and the two outer oxygen atoms a internet negative charge. Nonetheless, since the molecule is linear, these ii bond dipoles cancel each other out (i.due east. the vector add-on of the dipoles equals zilch) and the overall molecule has a zero dipole moment (\(\mu=0\)).
Although a polar bond is a prerequisite for a molecule to have a dipole, not all molecules with polar bonds showroom dipoles
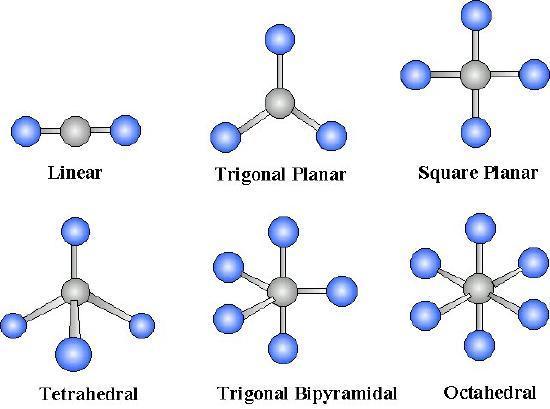
For \(AB_n\) molecules, where \(A\) is the central atom and \(B\) are however types of atoms, in that location are certain molecular geometries which are symmetric. Therefore, they volition accept no dipole fifty-fifty if the bonds are polar. These geometries include linear, trigonal planar, tetrahedral, octahedral and trigonal bipyramid.
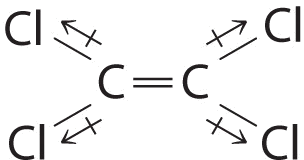
Example \(\PageIndex{3}\): \(\ce{C_2Cl_4}\)
Although the C–Cl bonds are rather polar, the individual bail dipoles cancel one another in this symmetrical structure, and \(\ce{Cl_2C=CCl_2}\) does non take a internet dipole moment.
Example \(\PageIndex{3}\): \(\ce{CH_3Cl}\)
C-Cl, the key polar bond, is 178 pm. Measurement reveals 1.87 D. From this data, % ionic character can be computed. If this bond were 100% ionic (based on proton & electron),
\[\begin{marshal} \mu &= \dfrac{178}{100}(4.80\; D) \nonumber \\[4pt] &= 8.54\; D \nonumber \end{align} \nonumber \]
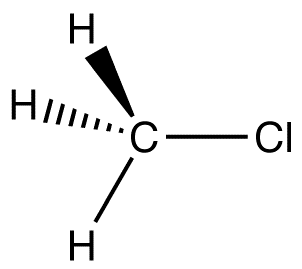
Although the bail length is increasing , the dipole is decreasing every bit yous motility down the halogen group. The electronegativity decreases every bit we movement down the grouping. Thus, the greater influence is the electronegativity of the two atoms (which influences the accuse at the ends of the dipole).
| Compound | Bond Length (Å) | Electronegativity Departure | Dipole Moment (D) |
|---|---|---|---|
| HF | 0.92 | 1.9 | 1.82 |
| HCl | one.27 | 0.nine | 1.08 |
| HBr | ane.41 | 0.7 | 0.82 |
| HI | 1.61 | 0.four | 0.44 |
References
- Housecroft, Catherine Eastward. and Alan Thou. Sharpe. Inorganic Chemistry. 3rd ed. Harlow: Pearson Didactics, 2008. Print. (Pages 44-46)
- Tro, Nivaldo J. Chemistry: A Molecular Approach. Upper Saddle River: Pearson Education, 2008. Print. (Pages 379-386)
Source: https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_%28Physical_and_Theoretical_Chemistry%29/Physical_Properties_of_Matter/Atomic_and_Molecular_Properties/Dipole_Moments
Post a Comment for "How Do You Know if a Bond Has a Dipole Moment"